•  

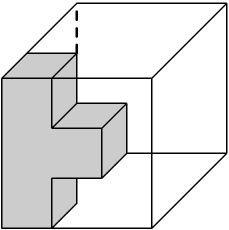
    he seven polyhedra in the diagram are formed by 27 identical cubes. Can these seven polyhedra be assembled into a larger cube with equal side lengths? And are there 240 different combinations? Here are the methods to assemble them into a larger cube:

    Place one polyhedron in the center, surrounded by the other six polyhedra.

    Rotate and arrange the polyhedra in various orientations to create different combinations.

    It is possible to form a larger cube by assembling the seven polyhedra in this manner. Additionally, there are 240 different combinations to achieve the desired result.

    upper layer

    middle layer

    lower layer

    4

    5

    2

    7

    5

    5

    7

    7

    6

    4

    1

    2

    4

    6

    2

    7

    6

    6

    1

    1

    2

    4

    3

    2

    3

    3

    3

     

    In addition to forming a cube, these polyhedra can also be arranged to create a variety of different shapes and patterns. Here are some examples:

    Furniture

    Animal

    Aeroplane

    For the purpose of research and documentation, Soma enthusiasts have assigned international standard numbers to each component (as shown in the diagram). Apart from the number 1, the remaining components are different combinations of four small cubes.

The Mathematics of Soma

When solving Soma puzzles, the most common approach is trial and error, relying on luck and guesswork. However, if one observes carefully and applies mathematical analysis, the task can be made much easier.

Let's take the example of constructing a cube. A cube has 6 faces, 8 vertices (corners), and 12 edges. Let's analyze the number of Soma components that can occupy each corner, starting with the vertices:

Number of components that can occupy a corner: [List the quantities for each corner]
By examining the possible combinations at each vertex, we can gain valuable insights into solving Soma puzzles efficiently.

Component number

1

2

3

4

5

6

7

Possible number of corners occupied

0 or 1

0 or 1 or 2

0 or 2

0 or  1

0 or 1

0 or 1

0 or 1

If component number 3 occupies 0 corners, then the remaining components can occupy a maximum of 1+2+1+1+1+1=7 corners altogether. This means it is not possible to construct a cube with 8 corners. Therefore, component number 3 must occupy 2 corners, indicating that it needs to be placed in an edge position.

Hence, component number 3 must occupy 2 corners, specifically in an edge location.

 

Students can challenge themselves by applying various analytical techniques and experimenting with different approaches. They can use the 27 small cubes to recreate the Soma puzzle pattern shown in the diagram.

Students are encouraged to use their creativity and problem-solving skills to assemble the cubes and replicate the given Soma pattern.