•  

    上圖的七塊立體是由27個大小相同的立方體組成?這七塊立體可拼砌成一個邊長為正立方體?且有240種不同的組合方法?以下是拼成一個正立方體的方法:

    上層

    中層

    下層

    4

    5

    2

    7

    5

    5

    7

    7

    6

    4

    1

    2

    4

    6

    2

    7

    6

    6

    1

    1

    2

    4

    3

    2

    3

    3

    3

     

    除了正方體外，亦可構成變化萬千的圖形如:

    傢俱

    動物

    飛機

    為了方便研究及記錄，索瑪迷把每片組件編上國際通用的號碼 (如上圖)，除了1號外，其餘的都是4個小立方體的不同組合?

索瑪裡的數學

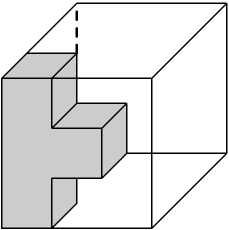
當我們用用索瑪拼圖時，最常用的方法是嘗試錯誤(Try and Error)，碰碰運氣? 但如果能細心觀察及作些數學分析，則事半功倍?

以拼成一個正方體為例?正立方體有6個面、8個頂點(角落)、12條邊。 以頂點開始分析，將索瑪的各組件能佔住角落的數量記下:

組件編號

1號

2號

3號

4號

5號

6號

7號

可能佔住角落數

0或1

0或1或2

0或2

0或1

0或1

0或1

0或1

如3號組件佔住0個角落，則其餘的組件合共最多能佔1+2+1+1+1+1=7個角落，這樣就無法拼出有8個角落的正立方體? 因此，3號組件必須佔住2個角落，即它必須放置在邊緣的位置上?

各同學不妨動下腦筋做各種分析，挑戰自己? 大家可利用27粒小立方塊自己動手依上圖樣式製作索瑪?